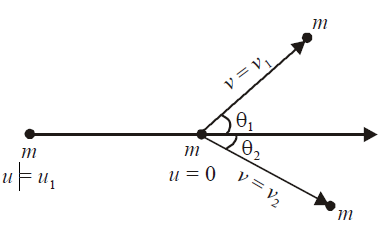
Q. Two spheres of equal mass collide with the collision being absolutely elastic but not central. Then the angle between the velocities ($\theta$) must be
Solution:
Since the given collision is elastic, so we can use both. The principles of conservation of linear momentum and conservation of kinetic energy. And as the mass of the two bodies are equal and considering one body to be initially at rest, we have
$u _{1}= v _{1} \cos \theta_{1}+ v _{2} \cos \theta_{2} \ldots$ (i)
$v _{1} \sin \theta_{1}= v _{2} \sin \theta_{2}$
$\Rightarrow v _{1} \sin \theta_{1}- v _{2} \sin \theta_{2}=0 \ldots$ (ii)
$u _{1}^{2}= v _{1}^{2}+ v _{2}^{2} \ldots$ (iii)
Squaring and adding (i) and (ii), we have
$v _{1}^{2}+ v _{2}^{2}+2 v _{1} v _{2}\left(\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}\right)= u _{1}^{2}$
$\Rightarrow \cos \left(\theta_{1}+\theta_{2}\right)=0$ using (iii)
$\Rightarrow \cos \theta=0$ where $\theta=\theta_{1}+\theta_{2}$
$\Rightarrow \theta^{\circ}=90$