Q.
Two solid bodies of equal mass $m$ initially at $T=0^{\circ} C$ are heated at a uniform and same rate under identical conditions. The temperature of the first object with latent heat $L_{1}$ and specific heat capacity in solid state $C_{1}$ changes according to graph 1 on the diagram. The temperature of the second object with latent heat $L_{2}$ and specific heat capacity in solid state $C_{2}$, changes according to graph 2 on the diagram. Based on what is shown on the graph, the latent heats $L_{1}$ and $L_{2}$ and the specific heat capacities $C_{1}$ and $C_{2}$ in solid state obey which of the following relationships?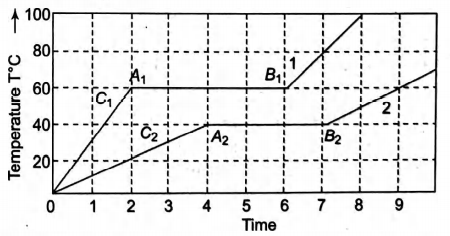
Thermal Properties of Matter
Solution: