Q.
Two solenoids A and B are coaxially place as shown in figure below.
The radius of inner and outer solenoids are $ {{R}_{1}} $ and $ {{R}_{2}} $ respectively and the numbers of turns per unit length are $ {{N}_{1}} $ and $ {{N}_{2}} $ respectively. Consider a length $ l $ of each solenoids, calculate the mutual inductance between them.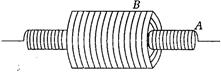
VMMC MedicalVMMC Medical 2015
Solution: