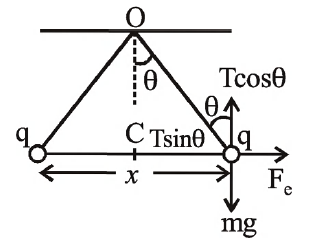
Q. Two small equal point charges of magnitude $q$ are suspended from a common point on the ceiling by insulating mass less strings of equal lengths. They come to equilibrium with each string making angle $\theta$ from the vertical. If the mass of each charge is $m$, then the electrostatic potential at the centre of line joining them will be $\left(\frac{1}{4\pi\,\in_{0}}=k\right).$
Solution:
In equilibrium, the expressions are given as,
$F = T \sin \theta$
(1)
$m g=T \cos \theta$
(2)
From above equations, it can be written as,
$\tan \theta=\frac{F}{m g}$
The electric force is given as,
$F =\frac{ q ^{2}}{4 \pi \varepsilon_{0} x ^{2}}$
Substitute the value of F in equation (3), we get
$\tan \theta=\frac{ q ^{2}}{4 \pi \varepsilon_{0} mgx ^{2}}$
$x =\sqrt{\frac{ q ^{2}}{4 \pi \varepsilon_{0} mg \tan \theta}}$
The electric potential is given as,
$V =\frac{ kq }{\frac{ x }{2}}+\frac{ kq }{\frac{ x }{2}}$
$V=\frac{4 k q}{x}$
$V=4 \sqrt{ kmg \tan \theta}$
Thus, the electric potential at the centre of the line is $4 \sqrt{ kmg \tan \theta}$.