Q.
Two simple pendulums $A$ and $B$ having lengths $l$ and $l / 4$ respectively are released from the position as shown in figure. The time after which the release of the two strings become parallel for the first time is ___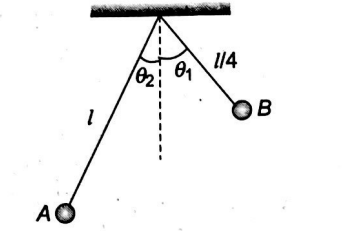
Oscillations
Solution:
