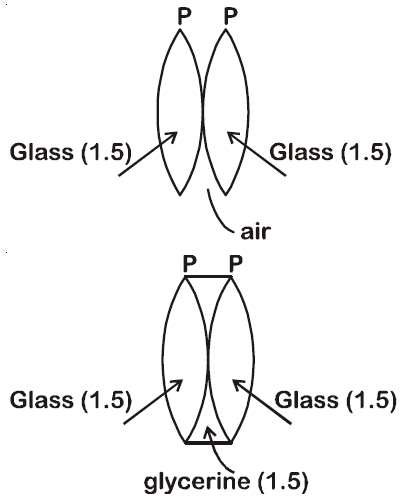
Q. Two similar thin $equi-convex$ lenses, of focal length $f$ each, are kept coaxially in contact with each other such that the focal length of the combination is $F_1$. When the space between the two lenses is filled with glycerin (which has the same refractive index $(p = 1.5)$ as that of glass) then the equivalent focal length is $F_2$. The ratio $F_1$ : $F_2$ will be :
Solution:
Equivalent focal length in air $\frac{1}{F_{1}} = \frac{1}{f} + \frac{1}{f} = \frac{2}{f} $
When glycerin is filled inside, glycerin lens behaves like a diverging lens of focal length (-f)
$ \frac{1}{F_{2}} = \frac{1}{f} + \frac{1}{f} - \frac{1}{f} $
$ = \frac{1}{f}$
$ \frac{F_{1}}{F_{2}} = \frac{1}{2} $