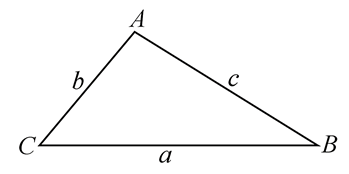
Question

Two sides of a triangle are given by the roots of the quadratic equation $x^{2}-2\sqrt{3}x+2=0$ and the angle between the sides is $\frac{\pi }{3}$ . The perimeter of the triangle is

• A. $2 \sqrt{3}$ units
• B. $\sqrt{6}$ units
• C. $2 \sqrt{3} + \sqrt{6}$ units
• D. $2 \left(\sqrt{3} + \sqrt{6}\right)$ units

Answer 1

Answer: (C)

Let the two sides $a$ and $b$ are the roots of the quadratic equation $x^{2}-2\sqrt{3}x+2=0$
.
$\therefore a+b=2\sqrt{3}$ and $ab=2$ . Also, $\angle C=\frac{\pi }{3}$
Using cosine rule,
$cosC=\frac{a^{2} + b^{2} - c^{2}}{2 a b}\Rightarrow \frac{1}{2}=\frac{a^{2} + b^{2} - c^{2}}{2 a b}$
$\Rightarrow a^{2}+b^{2}-c^{2}=ab\Rightarrow \left(a + b\right)^{2}-c^{2}=3ab$
$=>\left(2 \sqrt{3}\right)^{2}-c^{2}=3\times 2\Rightarrow c=\sqrt{6}$
$\therefore $ Perimeter $=a+b+c=2\sqrt{3}+\sqrt{6}$ units