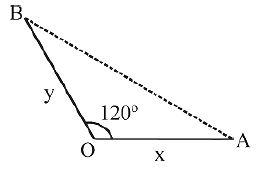
Q. Two ships $A$ and $B$ are sailing straight away from a fixed point $O$ along routes such that $\angle AOB$ is always $120^{\circ}$. At a certain instance, $OA = 8\, km, OB = 6\, km$ and the ship $A$ is sailing at the rate of $20\, km/hr$ while the ship $B$ sailing at the rate of $30 \,km/hr$. Then the distance between $A$ and $B$ is changing at the rate (in km/hr) :
Solution:
Let at any time t
$OA = x OB = y$
$\frac{dx}{dt} = 20\frac{dx}{dt} = 30$
$cos\left(120^{\circ}\right) = \frac{x^{2}+y^{2}-AB^{2}}{2xy}$
$AB^{2} = x^{2} + y^{2} + xy\ldots\left(1\right)$
d. w. r. to . t
$2\left(AB\right) \frac{d}{dt} \left(AB\right) = 2x \frac{dx}{dt} +2y \frac{dy}{dt}+2 \frac{dy}{dt}+y \frac{dx}{dt} \ldots \left(1\right)$
when $x = 8 \,y = 6$ then $AB = \sqrt{148}$ from $\left(1\right)$
So $\frac{d}{dt} \left(AB\right) = \frac{\left(2x \frac{dx}{dt} +2y \frac{dy}{dt}+ \frac{xdy}{dt}+y \frac{dx}{dt}\right)}{2\,AB}$
use $x = 8 y = 6 \,AB = \sqrt{148}$
$\frac{d}{dt} \left(AB\right) =260 / \sqrt{37}$