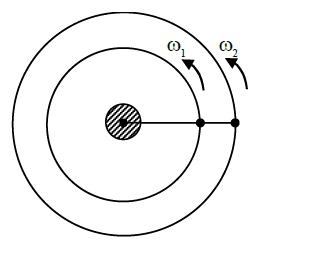
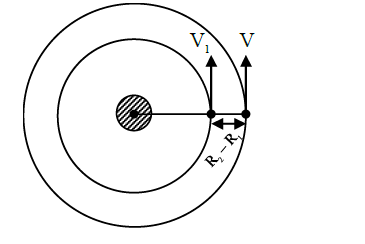
Question

Two satellites revolve around a planet in coplanar circular orbits in anticlockwise direction. Their period of revolutions are $1 $ hour and $8 $ hours respectively. The radius of the orbit of nearer satellite is $2 \times 10^{3} km$. The angular speed of the farther satellite as observed from the nearer satellite at the instant when both the satellites are closest is $\frac{\pi}{x} \text{rad} \,h^{-1}$ where $x$ is .....

Answer 1

$T _{1}=1$ hour
$\Rightarrow \omega_{1}=2 \pi \,rad /$ hour
$T _{2}=8$ hours
$\Rightarrow \omega_{2}=\frac{\pi}{4} \,rad /$ hour
$R _{1}=2 \times 10^{3} km$
As $T ^{2} \propto R ^{3}$
$\Rightarrow \left(\frac{ R _{2}}{ R _{1}}\right)^{3}=\left(\frac{ T _{2}}{ T _{1}}\right)^{2}$
$\Rightarrow \frac{ R _{2}}{ R _{1}}=\left(\frac{8}{1}\right)^{2 / 3}=4 $
$\Rightarrow R _{2}=8 \times 10^{3} km$

$V _{1}=\omega_{1} R _{1}=4 \pi \times 10^{3} \,km / h$
$V _{2}=\omega_{2} R _{2}=2 \pi \times 10^{3} \,km / h$
Relative $\omega=\frac{ V _{1}- V _{2}}{ R _{2}- R _{1}}=\frac{2 \pi \times 10^{3}}{6 \times 10^{3}}$
$=\frac{\pi}{3} rad /$ hour
$x =3$