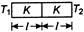
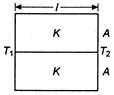
Q. Two rods of same material have same length and area. The heat $ \Delta Q $ flows through them for $12\, min$ when they are joint side by side. If now both the rods are joined in parallel, then the same amount of heat $ \Delta Q $ will flow in:
BHUBHU 2005Thermal Properties of Matter
Solution:
When two rods are joined, then the rate of flow of heat is given by
$ Q=KA\frac{({{\theta }_{1}}-{{\theta }_{2}})}{l}t $
where K is coefficient of thermal conductivity, A is area and I is length when rods are joined in series.
$ \Delta {{Q}_{1}}=\frac{A({{T}_{1}}-{{T}_{2}}){{t}_{1}}}{\frac{{{l}_{1}}}{{{K}_{1}}}+\frac{{{l}_{2}}}{{{K}_{2}}}} $
Given, $ {{l}_{1}}={{l}_{2}}=l,{{K}_{1}}={{K}_{2}}=K, $
we have $ \Delta {{Q}_{1}}=\frac{A({{T}_{1}}-{{T}_{2}}){{t}_{1}}}{\frac{l}{{{K}_{1}}}+\frac{l}{{{K}_{2}}}} $
$ =\frac{A({{T}_{1}}-{{T}_{2}}){{t}_{1}}}{l}\frac{K}{2} $
when rods are joined in parallel
$ \Delta {{Q}_{2}}=({{K}_{1}}A+{{K}_{2}}A)\frac{({{T}_{1}}-{{T}_{2}}){{t}_{2}}}{l} $
$ =2\frac{KA({{T}_{1}}-{{T}_{2}}){{t}_{2}}}{l} $
Given, $ \Delta {{Q}_{1}}=\Delta {{Q}_{2}} $
$ \therefore $ $ {{t}_{2}}=\frac{{{t}_{1}}}{4}=\frac{12}{4}=3\,\min $