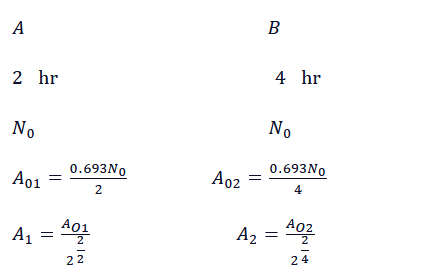Question

Two radioactive sources $A$ and $B$ of half lives $2\,hrs$ and $4\,hrs$ , respectively, initially contain the same number of radioactive atoms. At the end of $2\,hrs$ , their rates of disintegration will be in the ratio,

• A. $4:1$
• B. $2:1$
• C. $\sqrt{2}:1$
• D. None of these.

Answer 1

Answer: (C)

The number of atoms remaining after time $t\text{,}N=\frac{N_{0}}{2^{\left(t/T\right)}}$ ,
the radioactive disintegration constant, $\lambda =\frac{0 . 693}{T}$ .
Activity, $A=\lambda N$
$\Rightarrow A=\frac{0 . 693}{T}\frac{N_{0}}{2^{\left(t/T\right)}}$

$\frac{A_{1}}{ A_{2}}=\frac{A_{O 1}}{ A_{O 2}}\times \frac{\sqrt{2}}{2}$
$=\frac{\frac{0 . 693}{2} \cdot N_{0}}{\frac{0 . 693}{4} \cdot N_{0}}\times \frac{1}{\sqrt{2}}$
$=\frac{2}{\sqrt{2}}=\frac{\sqrt{2}}{1}$ .