1. Tardigrade
  2. Question
  3. Mathematics
  4. Two posts are x metres apart and the height of one is double that of the other. If from the mid-point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in metres) of the shorter post is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

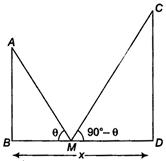
Q. Two posts are $ x $ metres apart and the height of one is double that of the other. If from the mid-point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in metres) of the shorter post is

Jharkhand CECEJharkhand CECE 2012

Solution:

Let the height of the shorter and the longer pole be $ h $ and $ 2h $ , respectively.
In $ \Delta ABM, $
$ \tan \theta =\frac{AB}{BM}=\frac{h}{x/2}=\frac{2h}{x} $ ... (i)
In $ \Delta CDM, $ $ \tan ({{90}^{o}}-\theta )=\frac{CD}{MD} $
$ =\frac{2h}{x/2}=\frac{4h}{x} $
$ \Rightarrow $ $ \cot \theta =\frac{4h}{x} $ ... (ii)
On multiplying both the equations, we get
$ 1=\frac{2h}{x}\cdot \frac{4h}{x} $
$ \Rightarrow $ $ \frac{{{x}^{2}}}{8}={{k}^{2}} $
$ \Rightarrow $ $ h=\frac{x}{2\sqrt{2}} $

Solution Image