Q.
Two point charges $q_x = -4 \,\mu C$ and $q_2 = 8\, \mu C$ are lying on the $y$-axis. They are equidistant from the point $P$, which lies on the $x$-axis. A small object of charge $q_0 = 8\, \mu C$ and mass $m = 12\, g$ is placed at $P$.
When it is released, what is its acceleration in $m \,s^{-2}$ ?
(Neglect the effect of gravity)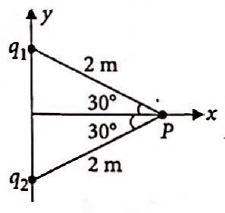
Electric Charges and Fields
Solution:
