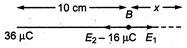
Q. Two point charges $ +36\mu C $ and $ -16\mu C $ are placed 10 cm apart. At a point $ X $ , there is no resultant force on unit positive charge. The distance of $ X $ from $ +36\mu C $ charge is
JamiaJamia 2010
Solution:
Both the charges are of opposite signs, so point $ X $ will not be in-between the charges.
At point $ X, $ there is no resultant force on unit charge, ie, electric field intensity is zero. $ {{E}_{1}}=k\frac{36\times {{10}^{-6}}}{{{(10+x)}^{2}}} $ (towards $ AX $ ) $ {{E}_{2}}=k\frac{16\times {{10}^{-6}}}{{{x}^{2}}} $ (towards $ XB $ or $ XA $ ) where, $ k=\frac{1}{4\pi {{\varepsilon }_{0}}}N{{m}^{2}}/{{C}^{2}} $ For intensity to be zero at point $ X $ . $ \therefore $ $ {{E}_{1}}={{E}_{2}} $ $ k=\frac{36\times {{10}^{-6}}}{{{(10+x)}^{2}}}=k\frac{16\times {{10}^{-6}}}{{{x}^{2}}} $ Or $ \frac{6}{10+x}=\frac{4}{x} $ $ \Rightarrow $ $ 6x=40+4x $ $ x=20\text{ }cm $ $ \therefore $ Distance of point $ X $ from $ +36\mu C=10+x $ $ =10+20=30\text{ }cm $