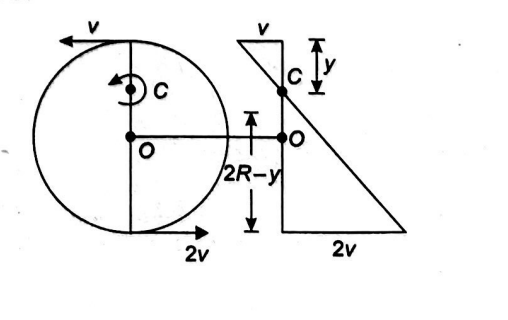
Q.
Two plates $1$ and $ 2$ move with velocities $-v$ and $2\, v$ respectively. If the sphere does not slide relative to the plates, assuming the masses of each body as $m$. If $m v^{2}=\frac{120}{123}$, then the kinetic energy of the system (plates $+$ sphere) is ___.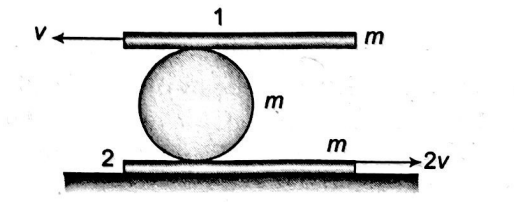
System of Particles and Rotational Motion
Solution: