Q.
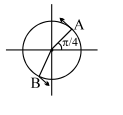
Two particles $P$ and $Q$ are executing SHM across same straight line whose equations are given as $y _{ P }= A \sin \left(\omega t +\phi_{1}\right)$ and $y _{ Q }= A \cos \left(\omega t +\phi_{2}\right)$. An observer, at $t =0$, observers the particle $P$ at a distance $A / \sqrt{2}$ moving to the right from mean position $O$ while $Q$ at $\frac{\sqrt{3}}{2}$ A moving to the left from mean position O as shown. Then, $\left(\phi_{2}-\phi_{1}\right)$ is equal to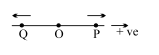
Oscillations
Solution: