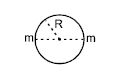
Question

Two particles of equal mass $'m'$ go around a circle of radius $R$ under the action of their mutual gravitational attraction. The speed of each partial with respect to their centre of mass is :

• A. $\sqrt{\frac{Gm}{4R}}$
• B. $\sqrt{\frac{Gm}{3R}}$
• C. $\sqrt{\frac{Gm}{2R}}$
• D. $\sqrt{\frac{Gm}{R}}$

Answer 1

Answer: (A)

$\frac{Gm^{2}}{\left(2R\right)^{2}} = m\omega^{2}R$
$\frac{Gm^{2}}{4R^{3}} = \omega^{2}$
$\omega = \sqrt{\frac{Gm}{4R^{3}}}$
$v = \omega R$
$v = \sqrt{\frac{Gm}{4R^{3}}}\times R\quad\quad= \quad\quad \sqrt{\frac{Gm}{4R}}$