Question

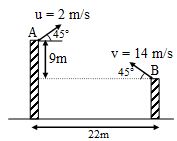
Two particles are simultaneously thrown from the top of two towers as shown. Their velocities are $2 \, m \, s^{- 1}$ and $14 \, m \, s^{- 1}$ . Horizontal and vertical separations between these particles are $22 \, m$ and $9 \, m$ respectively. Then the minimum separation between the particles in the process of their motion in meters is ( $g \, = \, 10 \, m \, s^{- 2}$ )

Answer 1

$v_x=8 \sqrt{2} \,m s ^{-1}=$ relative velocity along $x$-axis
$\therefore x=22-8 \sqrt{2} t$
$v_y=6 \sqrt{2} \,m / s =$ relative velocity
along the $y$-axis
$\therefore y=9-6 \sqrt{2} t$
$r=\sqrt{x^2+y^2}$
For minimum $r$,
$\frac{d r}{d t}=0 \Rightarrow t=\frac{23}{10 \sqrt{2}} s$
$r=\sqrt{x^2+y^2}$
substituting the value of $t$ in $r, r_{\min }$ $=6\, m$