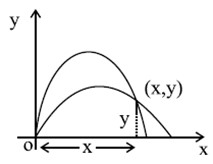
Question

Two particles are projected from a point at the same instant with velocities whose horizontal components and vertical components are $\left(u_{1} , v_{1}\right)$ and $\left(u_{2} , v_{2}\right)$ respectively. The time interval between their passing through the other common point of their path (other than origin) is

• A. $\frac{2}{g}\left(\frac{v_{1} u_{1} - v_{2} u_{2}}{u_{1} + u_{2}}\right)$
• B. $\frac{2}{g}\left(\frac{v_{1}^{2} + v_{2}^{2}}{u_{1} + u_{2}}\right)$
• C. $\frac{2}{g}\left(\frac{u_{1}^{2} + u_{2}^{2}}{v_{1} + v_{2}}\right)$
• D. $\frac{2}{g}\left(\frac{v_{1} u_{2} - v_{2} u_{1}}{u_{1} + u_{2}}\right)$

Answer 1

Answer: (D)

The time for particle 1 to pass through common point of their path
$t_{1}=\frac{x}{u_{1}}$
The time for particle 2 to pass through common point of their path
$t_{2}=\frac{x}{u_{2}}$
Difference of time $t=t_{1}-t_{2}$
Time $t=\frac{x}{u_{1}}-\frac{x}{u_{2}}=x\left(\frac{1}{u_{1}} - \frac{1}{u_{2}}\right)$
$y=xtan\theta -\frac{g x^{2}}{2 u_{x}^{2}}$
$y=x\frac{v_{1}}{u_{1}}-\frac{g x^{2}}{2 u_{1}^{2}}=x\frac{v_{2}}{u_{2}}-\frac{g x^{2}}{2 u_{2}^{2}}$
$\frac{v_{1}}{u_{1}}-\frac{v_{2}}{u_{2}}=x\frac{g}{2}\left(\frac{1}{u_{1}^{2}} - \frac{1}{u_{2}^{2}}\right)$
$\frac{v_{1}}{u_{1}}-\frac{v_{2}}{u_{2}}=x\frac{g}{2}\left(\frac{1}{u_{1}} + \frac{1}{u_{2}}\right)\left(\frac{1}{u_{1}} - \frac{1}{u_{2}}\right)$
$t=x\left(\frac{1}{u_{1}} - \frac{1}{u_{2}}\right)=\frac{2}{g}\left(\frac{v_{1} u_{2} - v_{2} u_{1}}{u_{1} + u_{2}}\right)$