Q.
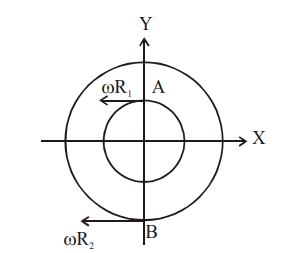
Two particles $A, B$ are moving on two concentric circles of radii $R_1$ and $R_2$ with equal angular speed $\Omega$. At $t = 0$, their positions and direction of motion are shown in the figure :
The relative velocity $\vec{\in}_A \, - \, \vec{\in}_B \, at \, t \, = \, \frac{\pi}{2 \Omega}$ is given by :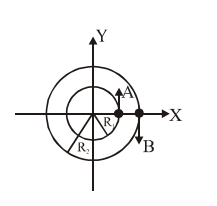
Solution:
$\theta \, = \, \omega t \, = \, \omega \frac{\pi}{2\omega} \, = \frac{\pi}{2}$
$\vec V_A \, - \, \vec V_S \, = \omega R_1 (-\hat{i}) \, - \omega R_2(-i)$