Q.
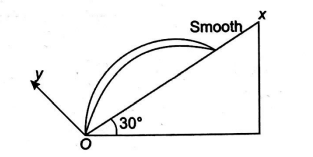
Two particles $A$ and $B$ are projected from point $O$ with equal speeds. They both hit the point $P$ of an inclined plane of inclination $15^{\circ}$. Particle $A$ is projected at an angle $30^{\circ}$ with inclined plane. If the ratio of time of flight of particles $A$ and $B$ is $1: \sqrt{n}$. The value of $n$ is _______.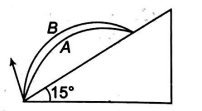
Motion in a Plane
Solution: