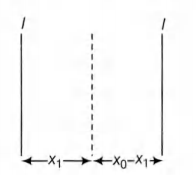
Q. Two parallel wires in the plane of the paper are distance $X_{0}$ apart. A point charge is moving with speed u between the wires in the same plane at a distance $X _{1}$ from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is $R_{1}$. In contrast, if the currents $I$ in the two wires have directions opposite to each other, the radius of curvature of the path is $R _{2} .$ If $\frac{ X _{0}}{ X _{1}}=3$, the value of $\frac{ R _{1}}{ R _{2}}$ is
Solution:

$B _{1}=\frac{1}{2}\left(\frac{\mu_{0}}{2 \pi}\right)\left(\frac{3 I }{ x _{0}}\right)$
$R _{1}=\frac{ mv }{ q B _{1}}$
$R _{2}=\frac{ mv }{ qB _{2}}$
$\Rightarrow \frac{ R _{1}}{ R _{2}}=\frac{ B _{2}}{ B _{1}}=\frac{1 / 3}{1 / 9}=3$