Q.
Two parallel plate capacitors A and B have the same
separation $d=8.85 \times 10^{-4}m $ between the plates. The plate
areas of A and B are $0.04m^2 $ and $0.02m^2 $ respectively. A slab
of dielectric constant (relative permittivity) K = 9 has
dimensions such that it can exactly fill the space between the
plates of capacitor B.
(a) The dielectric slab is placed inside A as shown in figure
(i) A is then charged to a potential difference of 110 V.
Calculate the capacitance of A and the energy stored in it
(b) The battery is disconnected and then the dielectric slab is
removed from A. Find the work done by the external
agency in removing the slab from A.
(c) The same dielectric slab is now placed inside B, filling it
completely. The two capacitors A and B are then
connected as shown in figure (iii). Calculate the energy
stored in the system.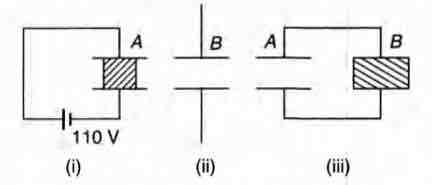
IIT JEEIIT JEE 1993Electrostatic Potential and Capacitance
Solution: