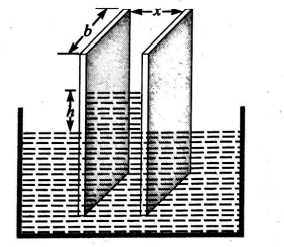
Question

Two parallel glass plates are dipped partly in the liquid of density ' $d$ ' keeping them vertical. If the distance between the plates is ' $x$ ', surface tension for liquids is $T$ and angle of contact is $\theta$, then rise of liquid between the plates due to capillary will be

• A. $\frac{T \cos \theta}{x d}$
• B. $\frac{2 T \cos \theta}{x d g}$
• C. $\frac{2 T}{x d g \cos \theta}$
• D. $\frac{T \cos \theta}{x d g}$

Answer 1

Answer: (B)

Let the width of each plate is $b$ and due to surface tension, liquid will rise upto height $h$. Then upward force due to surface tension $=2 T b \cos \theta$ ...(i)

Weight of the liquid that rises in between the plates
$=V d g=(b x h) d g$ ...(ii)
Equating (i) and (ii), we get $2 T \cos \theta=b x h d g$
$h=\frac{2 T \cos \theta}{x d g}$