Question

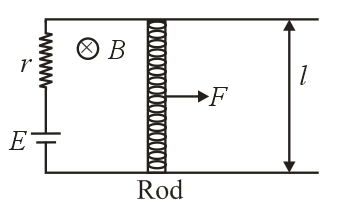
Two parallel conducting rails are connected to a source of emf $E$ and internal resistance $r.$ Another conducting rod of length $l$ having negligible resistance lies at rest and can slide without friction over the rails. A uniform magnetic field $B$ is applied perpendicular to the plane of the rails. At $t=0,$ the rod is pulled along the rails by applying a force $F.$ The velocity of the rod is observed to be $v=v_{0}cos\left(\omega t\right)$ then find the average power (in watt) spent by the force over $1$ cycle. (Given $B=2$ Tesla, $r=2\times 10^{- 4}\Omega,v_{0}=2 ms^{- 1},l=2cm$ )

Answer 1

$Blv-E-ir=0$
$F-ilB=m\frac{d v}{d t}\Rightarrow i=\frac{B l v - E}{r}$
$P_{a v g}=\frac{\displaystyle \int \overset{ \rightarrow }{F} \cdot \overset{ \rightarrow }{v} d t}{\displaystyle \int d t}$
$P_{a v g}=\frac{\displaystyle \int \left(m \frac{d v}{d t} + i l B\right) v d t}{\displaystyle \int d t}=\frac{\displaystyle \int \frac{l^{2} B^{2}}{r} v^{2} d t}{\displaystyle \int d t}$
$=\frac{v^{2} l^{2} B^{2}}{2 r}=\frac{4 \times 4 \times 10^{- 4}}{2 \times 2 \times 10^{- 4}}=4$