Question

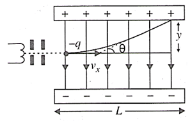
Two parallel charged plates are placed parallel to $x$ -axis. A particle of mass $m$ and charge $-q$ enters the region between the plates along the axis with a speed $v_{x}$ as depicted in the adjoining figure. If the length of the plates is $L$ and a uniform electric field $E$ is maintained between the plates, then find the vertical deflection of the particle at the far edge of the plate.

• A. $\frac{q E L^{2}}{2 m v_{x}^{2}}$
• B. $\frac{q E L_{ \, }^{2}}{2 m v_{x}}$
• C. $\frac{2 m v_{x}^{2}}{q E L^{2}}$
• D. $\frac{2 m v_{x}}{q E^{2} L}$

Answer 1

Answer: (A)

Here, in the vertical direction, initial velocity, $v=0$
acceleration, $a=\frac{F}{m}=\frac{q^{E}}{m} \, \left(\because \, \, F = \left(q E\right)^{ \, }\right)$
Time taken to cross the field, $t=\frac{d i s t a n c e}{v e l o c i t y}=\frac{L}{v_{x}}$
( $\because \, $ Velocity along the horizontal direction is constant)
$\because \, s=vt+\frac{1}{2}at^{2}$
$\because \, $ Deflection,
$y=0+\frac{1}{2}\left(\frac{q^{E}}{m}\right)\left(\frac{L}{v_{x}}\right)^{2}$
[Using (i) and (ii)]
$\therefore y=\frac{q E L^{2}}{2 m v_{x}^{2}}$