1. Tardigrade
  2. Question
  3. Physics
  4. Two paper screens A and B are separated by distance 100 m. A bullet penetrates A and B, at points P and Q respectively, where Q is 10 cm below P. If bullet is travelling horizontally at the time of hitting A, the velocity of bullet at A is nearly

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

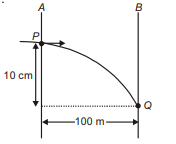
Q. Two paper screens $A$ and $B$ are separated by distance $100\, m$. A bullet penetrates $A$ and $B$, at points $P$ and $Q$ respectively, where $Q$ is $10\, cm$ below $P$. If bullet is travelling horizontally at the time of hitting $A$, the velocity of bullet at $A$ is nearly

Motion in a Plane

Solution:

$10\, cm \Rightarrow 10 \times 10^{-2} m$
$\Rightarrow 10^{-1} \Rightarrow 0.1\, m$
It is a case of horizontal projectile.
So, $a_{x}=0,\, u_{x}=4,\, u_{y}=0,\, a_{y}=-g$
$R=100\, m,\, T=\sqrt{\frac{2 H}{g}}$
$\Rightarrow $ Time of flight
$R=u_{x} T$
$100=u \sqrt{\frac{2 \times 0.1}{100}}$
$\Rightarrow \frac{u \sqrt{2}}{10}=100$
$u=\frac{1000}{\sqrt{2}}=707\, ms ^{-1}$

Solution Image