Q. Two organ pipes sounded together give $5$ beats per second. If their lengths are in the ratio of $50$ to $51$, then the frequency of shorter and longer pipes in Hz are respectively :
AFMCAFMC 2001
Solution:
Number of beats per second is equal to the difference of the frequencies of sound sources.
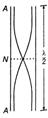
When air is blown from one end of an open pipe, a longitudinal wave travels from this end to the other. Since, pipe is open at both ends there is an antinode at each end. The distance between two consecutive antinodes is equal to half the wavelength. If $l$ be length of pipe and $\lambda$ be the wavelength, then
$l=\frac{\lambda}{2} \text { or } \lambda=2 l$
If $n_{1}$ be the freqency of note emitted from pipe, then
$n_{1}=\frac{v}{\lambda}=\frac{v}{2 l}$
Also number of beats per second (beat frequency)
$=n_{1}-n_{2}=$ difference of the frequencies of sound sources.
Given, $ n_{1}-n_{2}=5$
$\Rightarrow n_{1}=5+n_{2}$
$\therefore \frac{5+n_{2}}{n_{2}}=\frac{51}{50}$
$\Rightarrow n_{2}=250\, Hz$
and $ n_{1}=250+5=255\, Hz$
Since frequency $\propto \frac{1}{\text { length }}$
so, frequency of shorter pipe is $255\, Hz$ and that of longer pipe is $250\, Hz .$ of longer pipe is $250\, Hz$.