Q.
Two opposite forces $F_{1}=120 \, N$ and $F_{2}=80 \, N$ act on an elastic plank of modulus of elasticity $Y=2\times10^{11} N /m^{2} $ and length $l=1 m$ placed over a smooth horizontal surface. The cross-sectional area of the plank is $S=0.5$ $m^{2}$, The change in length of the plank is $x \times10^{-9} m$. The value of $x$ is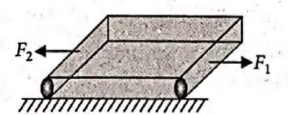
Mechanical Properties of Solids
Solution:
