Q. Two mutually perpendicular concentric current carrying coils have the same radius $2\pi cm$ . If currents $3A$ and $4A$ flow in each coil respectively, then calculate the magnitude of magnetic induction (in $Wb/m^{2}$ ) at the common centre of the two coils. $\left(\left(\mu \right)_{0} = 4 \pi \times \left(10\right)^{- 7} Wb A m^{- 1}\right)$
NTA AbhyasNTA Abhyas 2020
Solution:
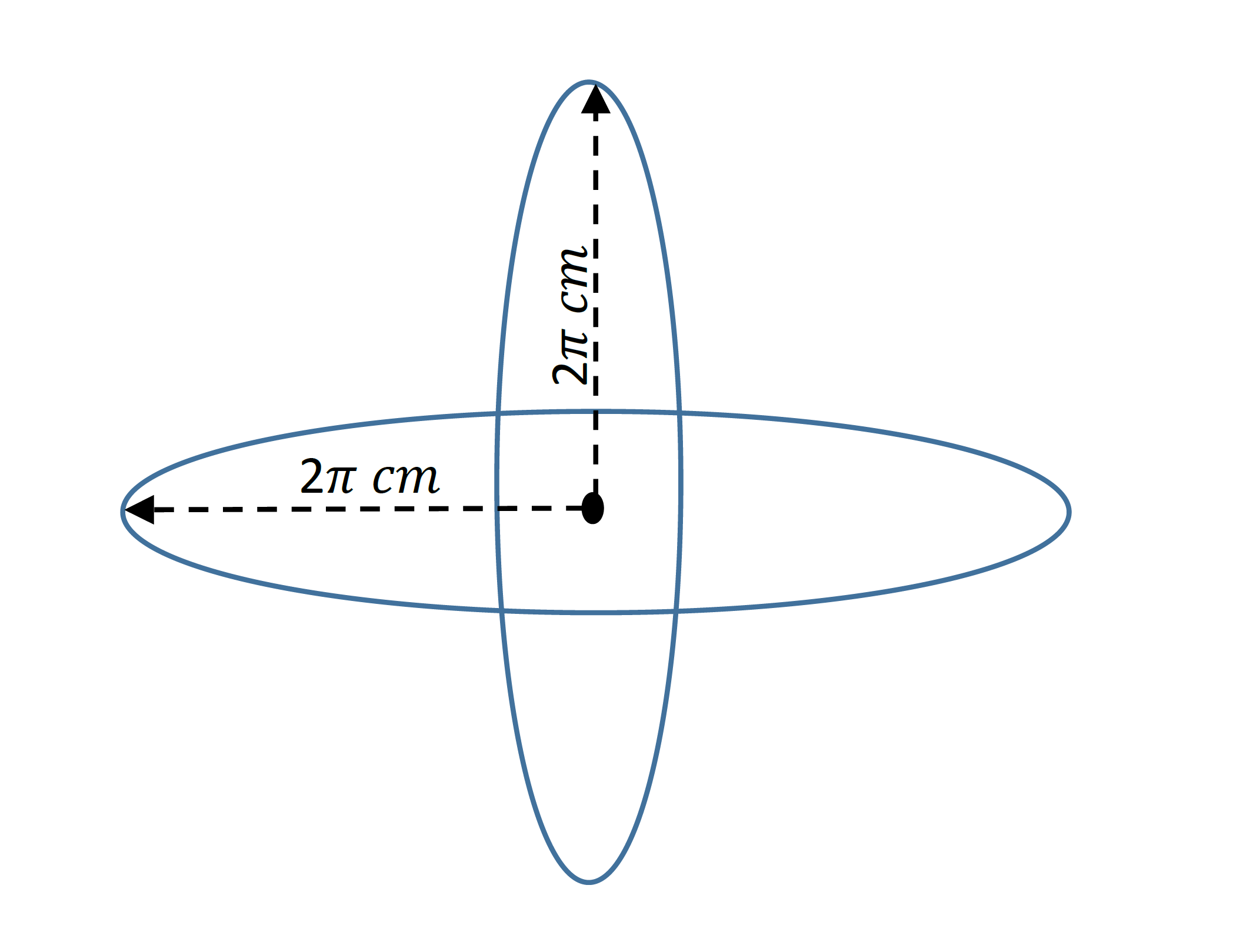
The magnetic field at the centre of a circular loop is given by;
$B=\frac{\mu _{0} i}{2 r}$
Thus,
$B_{1}=\frac{\left(\mu \right)_{0} i_{1}}{2 r}=\frac{\left(\mu \right)_{o} i_{1}}{2 \left(2 \pi \times \left(10\right)^{- 2}\right)}=\frac{\left(\mu \right)_{o} \times 3 \times \left(10\right)^{2}}{4 \pi }$
$B_{2}=\frac{\left(\mu \right)_{0} i_{2}}{2 r}=\frac{\left(\mu \right)_{o} i_{2}}{2 \left(2 \pi \times \left(10\right)^{- 2}\right)}=\frac{\left(\mu \right)_{o} \times 4 \times \left(10\right)^{2}}{4 \pi }$
Since $B_{1}$ and $B_{2}$ are perpendicular to each other, resultant magnetic field is;
$B_{n e t}=\sqrt{B_{1}^{2} + B_{2}^{2}}=\frac{\mu _{o}}{4 \pi }5\times 10^{2}$
$B_{n e t}=10^{- 7}\times 5\times 10^{2}$
$B_{n e t}=5\times 10^{- 5}Wb/m^{2}$

The magnetic field at the centre of a circular loop is given by;
$B=\frac{\mu _{0} i}{2 r}$
Thus,
$B_{1}=\frac{\left(\mu \right)_{0} i_{1}}{2 r}=\frac{\left(\mu \right)_{o} i_{1}}{2 \left(2 \pi \times \left(10\right)^{- 2}\right)}=\frac{\left(\mu \right)_{o} \times 3 \times \left(10\right)^{2}}{4 \pi }$
$B_{2}=\frac{\left(\mu \right)_{0} i_{2}}{2 r}=\frac{\left(\mu \right)_{o} i_{2}}{2 \left(2 \pi \times \left(10\right)^{- 2}\right)}=\frac{\left(\mu \right)_{o} \times 4 \times \left(10\right)^{2}}{4 \pi }$
Since $B_{1}$ and $B_{2}$ are perpendicular to each other, resultant magnetic field is;
$B_{n e t}=\sqrt{B_{1}^{2} + B_{2}^{2}}=\frac{\mu _{o}}{4 \pi }5\times 10^{2}$
$B_{n e t}=10^{- 7}\times 5\times 10^{2}$
$B_{n e t}=5\times 10^{- 5}Wb/m^{2}$