Q.
Two moles of helium gas undergo a cyclic process as shown
in figure. Assuming the gas to be ideal, calculate the
following quantities in this process.
(a) The net change in the heat energy.
(b) The net work done.
(c) The net change in internal energy.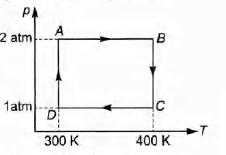
IIT JEEIIT JEE 1992Thermodynamics
Solution: