Q.
Two metal strips, one of brass and other of steel are of equal length $1.5\, m$ and equal thickness $0.25\, cm$. These are put together riveted and clamped at one end at $0^{\circ} C$ ae shown in fig. If the temperature rises to $50^{\circ} C$, calculate the radius of curvature (in meter) of the combined strip. $\alpha$ for brass is $19 \times 10^{-6}/{ }^{\circ} C , \alpha$ for steel $=11 \times 10^{-6} /{}^{\circ} C$.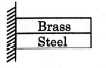
Thermal Properties of Matter
Solution:
