Q.
Two masses $M_1$ and $M_2$ are attached to the ends of string which passes over the pulley attached to the top of a double inclined plane. The angles of inclination of the inclined planes are $\alpha$ and $\beta$. If $M_1$ = $M_2$ and $\alpha$ = $\beta$, the acceleration of the system is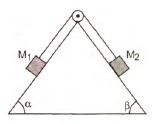
Laws of Motion
Solution:
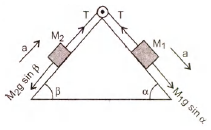
Figure shows a smooth double inclined plane. Two masses $M_1$ and $M_2$ are connected with a massless string passing over the pulley as shown in the figure. Let the mass $M_1$ be accelerating downwards at the rate $a$. Then the mass $M_2$ will accelerate at the same rate upwards. The equation of motion of $M_1$ will be
$M_1$ g sin $\alpha$ - T = $M_1$ a ...(1)
And that of mass $M_2$ will be
T - $M_2g$ sin $\beta$ = $M_2$ a .....(2)
To find a , we add equations (1) and (2) . That is :
$M_1g$ sin $\alpha - M_2g$ sin $\beta$ = $(M_1 + M_2) a$
This gives ; $a = \frac{M_1 \, sin \, \alpha - M_2 \, sin \, \beta}{M_1 + M_2}g$
To find tension T, we substitute the value of a in equation (1) and find :
$T = \frac{M_1M_2}{M_1+M_2} (sin\, \alpha + sin \, \beta) g$
If the double inclined plane itself is placed in a compartment accelerating at the rate f , then
$\overrightarrow{a} = \frac{M_1 \, sin \, \alpha - M_2 \, sin \, \beta }{M_1 + M_2} (\overrightarrow{g} - \overrightarrow{f})$ and $\overrightarrow{T} = \frac{M_1M_2}{M_1+M_2}(sin \, \alpha + sin \, \beta)(\overrightarrow{g} - \overrightarrow{f})$