Q.
Two masses $m_1$ = 5 kg and $m_2$ = 4.8 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when lift is free to move? (g = 9.8 $ms^{-2}$)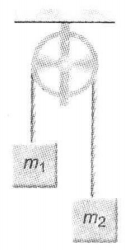
ManipalManipal 1980Laws of Motion
Solution:
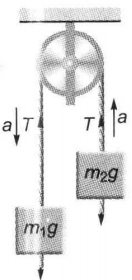
On releasing, the motion of the sxstem will be according to figure
$\, \, \, \, \, \, \, \, \, \, \, \, m_1 g - T = m_1 a \, \, \, \, \, \, \, \, \, \, \, \, \, ...(i)$
and $ \, \, \, \, \, \, \, \, \, \, \, T - m_2g = m_2 a \, \, \, \, \, \, \, \, \, \, \, \, ...(ii)$
On solving;
$ \, \, \, \, \, \, \, \, \, \, \, \, \, a =\bigg( \frac{m_1 - m_2}{m_1 + m_2} \bigg)g \, \, \, \, \, ...(iii)$
Given, $\, \, \, \, m_1 = 5 kg, m_2 = 4.8 kg,$
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, g = 9.8 ms^{-2}$
$\therefore \, \, \, \, \, \, a =\bigg( \frac{5 - 4.8}{5 + 4.8} \bigg) \times 9.8$
$ \, \, \, \, \, \, \, \, \, \, \, \, \frac{0.2}{9.8} \times 9.8 = 0.2 ms^{-2}$