Question

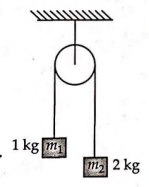
Two masses $m _1 = 1\, kg$ and $m_2 = 2\, kg$ are connected by a light inextensible string and suspended by means of a weightless pulley as shown in the figure. Assuming that both the masses start from rest, the. distance travelled by the centre of mass in two seconds is
(Take $g= 10\, ms^{-2}$)

• A. $\frac{20}{9} m$
• B. $\frac{40}{9} m$
• C. $\frac{2}{3} m$
• D. $\frac{1}{3} m$

Answer 1

Answer: (A)

Here, $m_1 = 1\,kg, m_2 = 2\,kg $
The acceleration of the system is
$a =\frac{\left(m_{2}-m_{1}\right)g}{m_{1} +m_{2}}=\frac{\left(2-1\right)g}{\left(1+2\right)} $
$=\frac{g}{3}=\frac{10}{3}$
Acceleration of the centre of mass is
$a_{cm} = \frac{m_{1}a_{1} +m_{2}a_{2} }{m_{1}+m_{2}} = \frac{1\left(-a\right)+2\left(a\right)}{1+2} $
$ = \frac{1\left(\frac{-g}{3}\right)+2\left(\frac{g}{3}\right)}{3} $
$ = \frac{g}{9} = \frac{10}{9}$
The distance travelled by the centre of mass in two seconds is
$S =\frac{1}{2}a_{cm}t^{2}$
$ = \frac{1}{2}\times\frac{10}{9} \times\left(2\right)^{2} $
$= \frac{20}{9} m$