Question

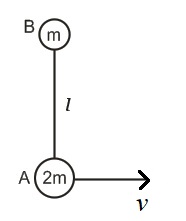
Two masses $A$ and $B$ connected with an inextensible string of length $l$ lie on a smooth horizontal plane. $A$ is given a velocity of $v \, m \, s^{- 1}$ along the ground perpendicular to line $AB$ as shown in the figure. Find the tension in a string during their subsequence motion.

• A. $\frac{2 m v^{2}}{3 l}$
• B. $\frac{3 m v^{2}}{2 l}$
• C. $\frac{m v^{2}}{2 l}$
• D. $\frac{4 m v^{2}}{3 l}$

Answer 1

Answer: (A)

From conservation of linear momentum
​ $\text{v}_{\text{cm}} = \frac{\text{m} \times 0 + \text{2mv}}{\text{m} + \text{2m}} \Rightarrow \text{v}_{\text{cm}} = \frac{\text{2v}}{3}$
position of the centre of mass
$\text{y}_{\text{cm}}=\frac{0 \times \text{2m} + \text{m} \times l}{\text{2m}}\Rightarrow \text{y}_{\text{cm}}=\frac{l}{3}$

velocity of $A$ in COM frame is $v _{ A }^{\prime}= v -2 v / 3 \quad \Rightarrow v _{ A }^{\prime}$
$= v / 3$
Tension will provide the required centripetal force
$T =\frac{(2 m ) v _{ A }^{2}}{(\ell / 3)} \Rightarrow T =\frac{(2 m )( v / 3)^{2}}{(\ell / 3)} \Rightarrow T =\frac{2 mv ^{2}}{3 \ell}$