Q.
Two masses $40\, kg$ and $30\, kg$ are connected by a weightless string passing over a frictionless pulley as shown in the figure. The tension in the string will be
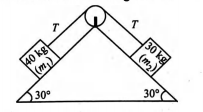
Laws of Motion
Solution:
