Q.
Two magnets of equal mass are joined at right angles to each other as shown. The magnet $1$ has a magnetic moment $3$ times that of magnet $2 .$ This arrangement is pivoted so that it is free to rotate in the horizontal plane. In equilibrium, what angle will the magnet $1$ subtend with the magnetic meridian?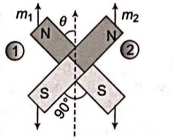
Magnetism and Matter
Solution: