Q.
Two long straight parallel wires are 2 m apart, perpendicular to the plane of the paper.
The wire A carries a current of 9.6 A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 10/11 m from the wire B, is zero.
Find
(a) The magnitude and direction of the current in B.
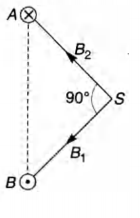
(b) The magnitude of the magnetic field of induction at the point S.
(c) The force per unit length on the wire B.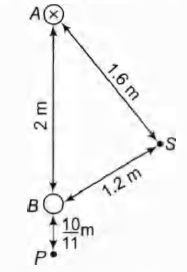
IIT JEEIIT JEE 1987Moving Charges and Magnetism
Solution:
(a) Direction of current at B should be
perpendicular to paper outwards. Let
current in this wire be $i_B.$ Then,
$\frac{\mu_0}{2\pi}\frac{i_A}{\Bigg(2+\frac{10}{11}\Bigg)}=\frac{\mu_0}{2\pi}\frac{i_B}{(10/11)}$
$or\, \, \, \, \, \, \, \, \, \, \frac{i_B}{i_A}=-\frac{10}{32}$
$or\, \, \, \, \, i_B=\frac{10}{32}\times i_A=\frac{10}{32}\times 9.6=3A$
(b) Since, $AS^2 + BS^2 = AB^2$
$\therefore \, \, \, \, \angle ASB=90^\circ$
At S : $B_1$ = Magnetic field due to $i_A$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \frac{\mu_0}{2\pi}\frac{i_A}{1.6}$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \frac{(2\times10^{-7})(9.6)}{1.6}$
$= 12 \times 10^{-7} T$
$B_2$ = Magnetic field due to $i_B$
$=\frac{\mu_0}{2\pi}\frac{i_B}{1.2}$
$\frac{(2\times10^{-7})(3)}{1.2}=5\times 10^{-7} T$
Since, $B_1 and B_2$ are mutually perpendicular. Net
magnetic field at 5 would be :
$B=\sqrt{B^2_1+B^2_2}$
$=\sqrt{(12\times10^{-7})^2+(5\times10^{-7})^2}$
$=13\times10^{-7} T$
(c) Force per unit length on wire B :
$\frac{F}{l}=\frac{\mu_0}{2\pi}\frac{i_A i_B}{r} (r = AB = 2 m)$
$=\frac{(2\times10^{-7)(9.6\times3)}{2}$
$= 2.88 \times 10^{-6} N/m$