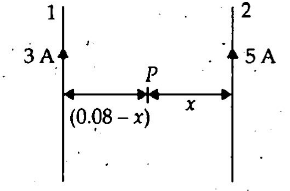
Q. Two long parallel wires placed $0.08 \, m$ apart carry currents $3 \, A $ and $5 \, A$ in the same direction. The distance from the conductor carrying larger current where the resultant magnetic field is zero is
Solution:
Let $P$ be the point where magnetic field is zero. Its distance from wire $2$ is $x$.
Magnetic field at point $P$ due to wire $1 \, \bar{B}_1 = \frac{\mu_0(3)}{2 \pi (0.08 - x)} \otimes$
Magnetic field at point $P$ due to wire 2 $1 \, \bar{B}_2 = \frac{\mu_0(5)}{2 \pi x} \odot$
Here, $\vec{B}_P = \vec{B}_1 + \vec{B}_2 = 0 $
or , $| \vec{B}_1 | = | \vec{B}_2 |$
$\frac{\mu_0 (3)}{2 \pi (0.08 - x)}| = \frac{\mu_0 (5)}{2 \pi x}$
or $3x = 5(0.08 - x) $
or $8x = 0.4 $
or $x = 0.05 m $