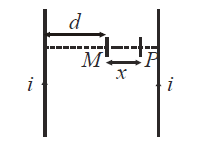
Question

Two long parallel wires carry equal current $i$ flowing in the same direction are at a distance $2d$ apart. The magnetic field $B$ at a point lying on the perpendicular line joining the wires and at a distance $x$ from the midpoint is -

• A. $\frac{\mu_{0} i d}{\pi\left(d^{2}+x^{2}\right)}$
• B. $\frac{\mu_{0} i x}{\pi\left(d^{2}-x^{2}\right)}$
• C. $\frac{\mu_{0} i x}{\left(d^{2}+x^{2}\right)}$
• D. $\frac{\mu_{0} i d}{\left(d^{2}+x^{2}\right)}$

Answer 1

Answer: (B)

The magnetic field due to two wires at $P$
$B_{1}=\frac{\mu_{0} i}{2 \pi(d+x)} ; B_{2}=\frac{\mu_{0} i}{2 \pi(d-x)}$
Both the magnetic fields act in opposite direction.
$\therefore B=B_{2}-B_{1}$
$=\frac{\mu_{0} i}{2 \pi}\left[\frac{1}{d-x}-\frac{1}{d s+x}\right] $
$=\frac{\mu_{0} i}{2 \pi}\left[\frac{d+x-d+x}{d^{2}-x^{2}}\right]$
$=\frac{\mu_{0} i x}{\pi\left(d^{2}-x^{2}\right)} .$