Question

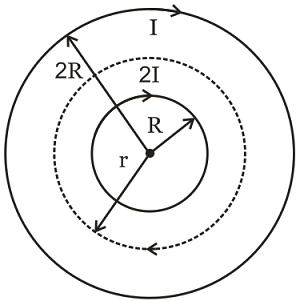
Two long coaxial solenoids of radius $R$ and $2R$ have equal number of turns per unit length. They carry time-varying currents $i_{1}=2kt$ and $i_{2}=kt$ respectively, in the same direction. A point charge released between the solenoids at a distance $r$ , is seen to move along a circular path. Then the value of $r$ is

• A. $r=R\sqrt{2}$
• B. $r=3 R/2$
• C. $r=R\sqrt{3}$
• D. It can be any value between $R$ and $2R$

Answer 1

Answer: (A)

The magnetic field due to the inner solenoid (within its volume) is
$B_{1}=\left(\mu \right)_{0}n\left(2 k t\right)$
The magnetic field due to the outer solenoid (within its volume) is
$B_{2}=\left(\mu \right)_{0}n\left(k t\right)$
The flux of magnetic field through the circular area of radius $r$ is
$\phi=B_{1}\pi R^{2}+B_{2}\pi r^{2}$
$\Rightarrow \phi=\pi \left(\mu \right)_{0}nkt\left(2 R^{2} + r^{2}\right)$
If $\overset{ \rightarrow }{E}$ is the induced electric field at $r$ , then
$\oint\overset{ \rightarrow }{E}.d\overset{ \rightarrow }{r}=-\frac{d \phi}{d t}$
$\Rightarrow E\times 2\pi r=\pi \left(\mu \right)_{0}nk\left(2 R^{2} + r^{2}\right)$
$\Rightarrow E=\left(\mu \right)_{0}nk\left(\frac{R^{2}}{r} + \frac{r}{2}\right)$
The radius of the circle traversed by the charged particle is
$r=\frac{m v}{q B_{2}}$
$v=E\frac{q t}{m}=\left(\mu \right)_{0}nk\left(\frac{R^{2}}{r} + \frac{r}{2}\right)\frac{q t}{m}$
$\Rightarrow \left(\mu \right)_{0}nk\left(\frac{R^{2}}{r} + \frac{r}{2}\right)\frac{q t}{m}=\frac{q r B_{2}}{m}$
$\Rightarrow \left(\mu \right)_{0}nkt\left(\frac{R^{2}}{r} + \frac{r}{2}\right)=r\left(\mu \right)_{0}nkt$
$\Rightarrow R^{2}+\frac{r^{2}}{2}=r^{2}$
$\Rightarrow r=R\sqrt{2}$