Q.
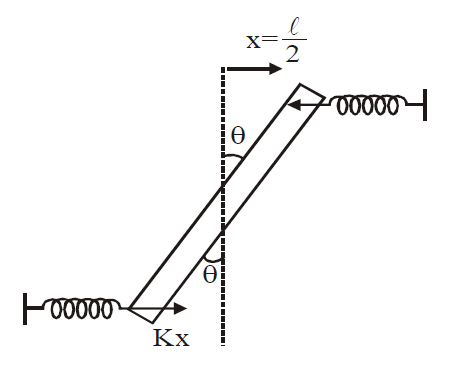
Two light identical springs of spring constant. $k$ are attached horizontally at the two ends of a uniform horizontal rod $AB$ of length $'l'$ and mass $'m'$. The rod is pivoted at its centre $'O'$ and can rotate freely in horizontal plane. The other ends of the two springs are fixed to rigid supports as shown in figure. The rod is gently pushed through a small angle and released. The frequency of resulting oscillation is: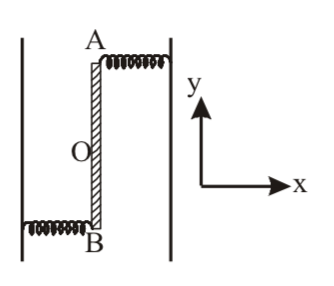
Solution:
$\tau =-2 Kx \frac{\ell}{2} \cos\theta $
$ \Rightarrow \tau =\left(\frac{K\ell^{2}}{2}\right)\theta =- C\theta$
$ \Rightarrow f= \frac{1}{2\pi} \sqrt{\frac{C}{I}} = \frac{1}{2\pi} \sqrt{\frac{\frac{k\ell^{2}}{2}}{\frac{M\ell^{2}}{12}}} $
$ \Rightarrow f= \frac{1}{2\pi} \sqrt{\frac{6K}{M }}$