Question

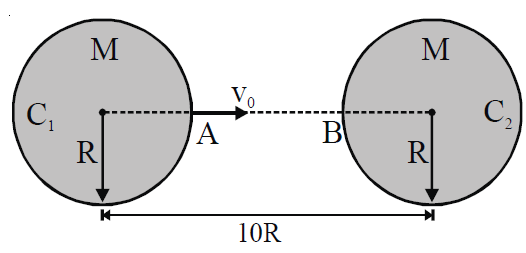
Two large spherical objects of mass $M$ each (uniformly distributed) are fixed as shown in the figure. A small point mass $m$ is projected from point $A$ heading towards centre $C_{2}$ of the second sphere. The minimum velocity of point mass so that it can reach up to the second object at point $B$ is $\frac{n}{3}\sqrt{\frac{G M}{5 R}}$ . Then calculate $n$ . [Neglect other gravitational forces]

Answer 1

If the ball can reach the mid point of line connecting spheres, then it will get attracted towards B. (At midpoint gravitational intensity is zero)
Using energy conservation,
$\frac{1}{2}mV_{0}^{2}-\frac{G M m}{R}-\frac{G M m}{9 R}=-2\frac{G M m}{5 R}+0$
Solving, $V_{0}=\frac{8}{3}\sqrt{\frac{G M}{5 R}}$
$\Rightarrow n=8$