Q.
Two large circular discs separated by a distance of $0.01\, m$ are connected to a battery via a switch as shown in the figure. Charged oil drops of density $900\, kg \,m ^{-3}$ are released through a tiny hole at the center of the top disc. Once some oil drops achieve terminal velocity, the switch is closed to apply a voltage of $200\, V$ across the discs. As a result, an oil drop of radius $8 \times 10^{-7} m$ stops moving vertically and floats between the discs. The number of electrons present in this oil drop is (neglect the buoyancy force, take acceleration due to gravity $=10 \,ms ^{-2}$ and charge on an electron $(e) =1.6 \times 10^{-19} C$ )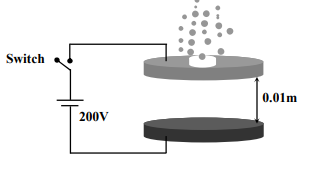
JEE AdvancedJEE Advanced 2020
Solution: