Q.
Two identical uniform discs roll without slipping on two different surfaces AB and CD (see figures) starting at A and C with linear speeds $ν_1$ and $ν_2$, respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed and $ν_1 = 3m/s$, then $ν_2$ in m/s is $(g = 10 m/s^2)$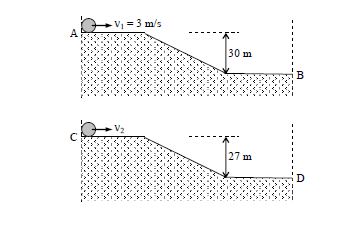
JEE AdvancedJEE Advanced 2015
Solution: