Q.
Two identical springs of spring constant k are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be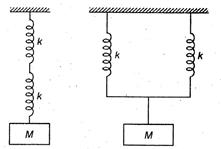
Jharkhand CECEJharkhand CECE 2007
Solution: