Q.
Two identical spherical balls of mass $M$ and radius $R$ each are stuck on two ends of a rod of length $2R$ and mass $M$ (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is :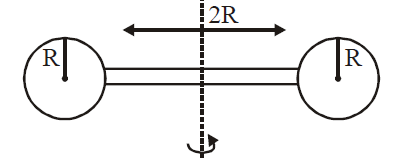
Solution: