Question

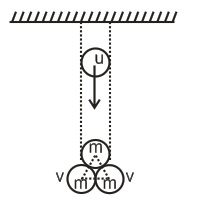
Two identical spheres, each of mass $m$ are suspended by vertical strings such that they are in contact with their centres at the same level. A third identical sphere strikes the other two spheres simultaneously with a velocity $u$ such that the centres of the spheres at the instant of impact form an equilateral triangle in a vertical plane. If the collision is perfectly elastic, then the combined impulse due to the strings is

• A. $\frac{12}{7}mu$
• B. $\frac{6}{7}mu$
• C. $\frac{2 \sqrt{3}}{7}mu$
• D. $\frac{8}{7}mu$

Answer 1

Answer: (A)

Let us assume that after the collision, the velocity of the incoming ball changes from $u$ to $u^{'}$ and the other two balls move in the opposite directions with the same speed $v$ , then
$-2\left(N \Delta t\right)cos30^\circ =mu^{'}-mu$
$\Rightarrow -\left(N \Delta t\right)\sqrt{3}=mu^{'}-mu$
For the ball attached to the string,
$\left(N \Delta t\right)sin30^\circ =mv$
$\Rightarrow N\Delta t=2mv$
Eliminating $N\Delta t$ , we obtain
$-2\sqrt{3}mv=mu^{'}-mu$
Using the coefficient of restitution equation we get
$1=\frac{v cos 60 ^\circ - u^{'} cos 30 ^\circ }{u cos 30 ^\circ }$
$\Rightarrow \sqrt{3}u=v-\sqrt{3}u^{'}$
$\Rightarrow 2\sqrt{3}v=6u+6u^{'}$
$6u+6u^{'}=u-u^{'}$
$\Rightarrow u^{'}=-\frac{5}{7}u$
The total impulse of tension is
$-2T\Delta t=mu^{'}-mu$
$2T\Delta t=m\frac{5 u}{7}+mu=\frac{12}{7}mu$