Question

Two identical small masses each of mass $m$ are connected by a light inextensible string on a smooth horizontal floor. A constant force $F$ is applied at the mid point of the string as shown in the figure. The acceleration of each mass towards each other is,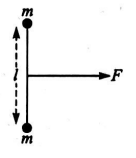

• A. $\frac{F}{2 \sqrt{3} m}$
• B. $\frac{\sqrt{3} F}{2 m}$
• C. $\frac{2}{\sqrt{3}} \frac{F}{m}$
• D. None of these

Answer 1

Answer: (A)

Let the tension in the string be $T$ at any angular position $\theta$, the acceleration of each ball along $x$ and $y$ axes be $a$ and $a_{1}$ respectively.
Writing the equation of motion of $m$, we obtain
$\Sigma F_{x}=m a$
$\Rightarrow T \cos \theta=m a$ ...(1)
$\Sigma F_{y}=m a_{1}$
$\Rightarrow T \sin \theta=m a_{1}$ ...(2)
At point $P$, as it is accelerating with an acceleration a, therefore
$F-2 T \cos \theta=m_{p}\, a$
where $m_{p}=$ mass of the string at the point $P \cong 0$
$\Rightarrow F=2 T \cos \theta$ ...(3)
$(2)+(1) \Rightarrow \tan \theta=\frac{a_{1}}{a}$
$\Rightarrow a_{1}=a \tan \theta$
where $a=\frac{T \cos \theta}{m}$ from (1).
Putting $T=\frac{F}{2 \cos \theta}$, from (3), we obtain
$a_{1}=\frac{F}{2 m} \tan \theta$
Putting $\theta=30^{\circ}$
$\Rightarrow a_{1}=\frac{F}{2 \sqrt{3} m}$